Copper Mass Number
What is the mass of one atom of copper in grams?
- Atomic Mass Number Copper
- Mass Number Of Copper 64
- Isotope Copper 62 Mass Number
- Copper Mass Number Rounded
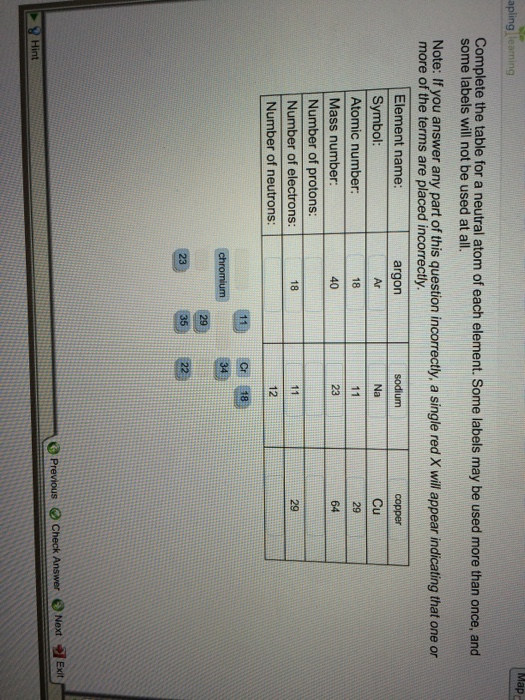
Keeping this in view, how many protons neutrons and electrons does copper have? Copper has an atomic number of 29, so it contains 29 protons and 29 electrons. The atomic weight (sometimes called atomic mass) of an atom is approximated by the sum of the number of protons and the number of neutrons in the nucleus of the atom. Copper, isotope of mass 64 Please visit the Copper element page for information specific to the chemical element of the periodic table.
1 Answer
Explanation:
1 atom of copper must be converted in moles to express it as a quantity that can be converted into grams (our second step).
Avogadro's Number
Related questions
By: Krishna Sinha
Lab Partners: Nicholas Chang and Brendan Morey
Purpose:
The purpose of this study was to utilize a colorimeter, dilution and molarity concepts with copper nitrate, and depth to determine the amount of copper by mass in a brass sample. A secondary purpose was to demonstrate Beer’s law.
Introduction
Copper nitrate can be formed with the addition of copper metal to nitric acid (HNO3), as seen through the following reaction:
Cu2+ + 2HNO3 forms Cu(NO3)2 + H2
Using spectrophotometry, the chemical composition of any substance can be calculated. This concept and molar concentration amalgamate into what is known as Beer’s Law, which states that the absorbance value of a solution is directly proportional to the molar concentration (moles solute/Liters solution). In this study, the concept of dilution (M1V1=M2V2) was used to generate copper nitrate solutions with different concentrations. Beer’s law was graphed as the absorbance value of each solution was determined using a colorimeter set to 635 nm, the predetermined optimal wavelength to test absorbance of the blue copper nitrate solutions.
Additionally, the molarity of a solution can be calculated using judgment of color by the naked eye and depth. Using a substance of known concentration and one of unknown concentration, the naked eye can judge when the colors of each solution look the same, take the individual depths of the known and unknown, and utilize the equation M1D1=M2D2.
This study determined the amount of copper by mass in a sample of brass using concentration values calculated by the naked eye and depth, while also demonstrating Beer’s law.
Procedure 1: Dilutions
- Obtain a 10 mL graduated cylinder, and fill it with 10 mL of a .4 M solution of copper nitrate.
- Pipette this solution into a small cuvette until the cuvette is 3/4 full. Tightly cap the cuvette and label the concentration of the sample.
- To make a .2 M, .1M, .05 M, and .025 M, utilize the dilution equation: M1V1=M2V2. Given that M1 (for the first time) equals .4 M with the given volume being 10 mL, calculate the volume of a .4 M solution needed to make a .2 M solution.
- Once the volume has been calculated, pipette out extra mL of the solution. Refill the graduated cylinder back up to 10 mL with distilled water.
- Repeat steps 2 and 3 each time, making sure that distilled water is used each time and that any excess mL of a solution is pipetted into a waste beaker.
Procedure 2: Making the Copper Nitrate Solution of Unknown Concentration
- Acquire a brass sample between 1-2 grams. Record this mass.
- Assuming that the brass is completely composed of copper, calculate the necessary amount of nitric acid needed to completely react with the copper, using the chemical equation in the introduction.
- To make sure that the nitric acid is in excess, add 2 more mL. Make sure all ntiric acid reactions are carried out under the flame hood.
- Pour the nitric acid onto the brass. Make sure it is completely reacted.
- Obtain a 100 mL volumetric flask, and pour the copper nitrate solution in. Do not fill it to the 100 mL mark. Pour distilled water until the solution reaches 100 mL.
- Pour this solution into a cuvette label it with a variable for the unknown.
- After calibration, take the absorbance value of the unknown.
Procedure 3: Data Collection and Calculations
- Obtain a colorimeter and set the wavelength to 635 nm. This will be the optimal wavelength for the blue copper nitrate solutions.
- Obtain a LabQuest unit and connect it to the colorimeter. Calibrate the colorimeter with a blank cuvette ( a cuvette filled with only distilled water). Make sure that the absorbance value reads 0.
- For each of the solutions (starting with the least concentrated solution), determine the absorbance value for each diluted solution prepared. A graph should be generated plotting absorbance v. molar concentration.
- After all molar concentration absorbance values have been obtained, take the absorbance value of the unknown.
- For the unknown solution, obtain 2 test tubes, one with a .4 M solution of copper nitrate, and one with the unknown. Looking right over the top of each test tube, use 2 different pipettes to equalize the color of the .4 M solution and the unknown.
- When the solutions are of equal color, take a ruler and measure the depths of the known and unknown. Determine the unknown concentration using M1D1=M2D2.
- With the given concentration of the unknown determined, use the
Data
Mass of Brass: 1.14515 g
| Concentration | Absorbance |
| .400 M | 0.927 |
| .200 M | 0.316 |
| .100 M | 0.219 |
| .050 M | 0.2 |
| .025 M | 0.125 |
Table 1.0: This table displays the absorbance values obtained for the copper nitrate solutions of known concentration.
Note 1: Distilled water was not used in these calculations, making the formation of nominal amounts of other compounds within the copper nitrate solutions possible.
Note 2: As the lack of distilled water had a marginal effect on results, the following displays the final calculations. Originally there was a discrepancy in concentration values for the .025 and .05, along with the .1 and .2 solutions; however, this is most likely attributed to movement during cleanup and storage.
| Depth of .4 M solution | 4.1 cm |
| Depth of unknown solution | 12.5 cm |
Table 2.0: The following table displays the obtained depths for each solution, which were used to calculate the concentration of the unknown solution.
Analysis
This figure displays the absorbance values for copper nitrate solutions of known concentration. As clearly seen, Beer’s law is validated as the absorbance increases with the concentration.
Atomic Mass Number Copper
Calculations
This figure displays the calculations made to find the percentage of copper by mass in the original brass sample. Using the acquired concentration from M1D1=M2D2 and known volume of solution, the mole amount of copper was calculated, converted to grams using the molar mass, and put it over the original brass mass.

This figure is an extension problem on the lab, demonstrating an understanding of the Beer’s law and chemical composition.
Mass Number Of Copper 64
Conclusion:
Isotope Copper 62 Mass Number
Overall, the purpose of the lab was met, as we were able to use spectrophotometry to demonstrate Beer’s lab, and were able to use color and depth to calculate the molar concentration of the unknown solution (.1312 M), therefore giving us a mole amount, mass (.834 g), and percentage (72.83%).
Errors in the lab might have arisen from lack of distilled water in the prepared solutions, as nominal amounts of other compounds might have been formed within each solution, therefore partially skewing the absorbance values.
Copper Mass Number Rounded
Overall, the color method determined a more accurate reading, as opposed to plugging the absorbance value into a linear equation, as we were able to carefully determine the molar concentration through M1D1=M2D2.
